Diffusione nel percorso tra la lampada e la superficie

La quantità di luce che viene diffusa dalle particelle dell'atmosfera cresce in modo esponenziale con il cammino ottico percorso dalla luce. Vedremo più avanti i meccanismi del fenomeno della diffusione della luce da parte delle particelle atmosferiche. La quantità di luce dI che subisce diffusione in un percorso infinitesimo dz è data da: $$dI=-I N \sigma dz$$

(5)

ove N è il numero di particelle per unità di volume che provocano la diffusione, $\sigma$ è la loro sezione d'urto integrata ed I è l'intensità della luce incidente.

   

$$\beta_{sc}$$ Condizioni meteorologiche Visibilità km^-1

$$< \gt$$ nebbia densa

nebbia spessa 50m - 200m 78.2-19.6

nebbia moderata 200m-500m 19.6-7.82

nebbia leggera 500m-1000m 7.82-3.91

nebbia sottile 1km-2km 3.91-1.96

foschia 2km-4km 1.96-0.954

foschia leggera 4km-10km 0.954-0.391

limpido 10km-20km 0.391-0.196

molto limpido 20km-50km 0.196-0.078

$$\gt \gt$$ eccezionalmente limpido

(aria pura) (277km) (0.0141⁽¹⁾ )

Note:
Da Hulburt (1941).
Per confronto è riportato il valore del coefficiente di diffusione molecolare dell'aria pura, senza aerosoli .

La frazione di luce $\eta$ che ha subito diffusione in un percorso di lunghezza d è quindi: $$\eta=\frac{I_{diffusa}}{I_{0}}=\left(1-e^{(-N \sigma d)}\right)$$

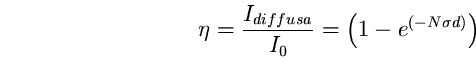
(6)

La frazione di luce diffusa cresce in modo esponenziale con la lunghezza d del percorso.

Se una lampada illumina dall'alto in basso con un fascio non molto inclinato rispetto la verticale, una buona parte della radiazione diffusa raggiunge lo stesso il suolo a causa della tendenza delle particelle a diffondere la luce in una direzione vicina alla direzione originaria del flusso di luce (Front Scattering). Vedremo più in dettaglio in seguito questo fenomeno, ma l'effetto principale per percorsi brevi consiste in un allargamento del fascio. Se però il fascio punta dal basso verso l'alto come accade talvolta nell'illuminazione di pareti di edifici, oppure forma un angolo ampio con la verticale come in alcuni impianti sportivi, l'allargamento del fascio prodotto dalla diffusione fa andare una parte consistente della luce in cielo.

La quantità di luce riflessa o diffusa nella direzione opposta rispetto la direzione di incidenza (Backscattering) è piccola ma non è trascurabile quando il percorso della luce non è breve e quando la concentrazione di aerosoli  nelle vicinanze del suolo è elevata (es. presenza di umidità, bruma, foschia). Consideriamo, ad esempio, una torre faro  alta 30 metri. Possiamo stimare con la formula precedente la percentuale della luce emessa che viene diffusa dalle particelle atmosferiche. Assumiamo che la concentrazione e la sezione d'urto degli aerosoli  a livello del suolo siano tali che il loro prodotto $N\sigma=\beta_{sc}$ chiamato coefficiente di diffusione sia dell'ordine di 10^-5 cm^-1 al suolo, come avviene tipicamente nel caso di foschia. Per semplificare il calcolo, assumiamo inoltre che il percorso della luce sia di 30 metri, trascurando le differenze dovute al diverso angolo di emissione. Applicando la formula si ottiene che circa il 3% della luce emessa dalla torre faro viene diffusa. Assumiamo ora che le particelle diffondano nell'emisfero centrato nella direzione opposta rispetto alla direzione della luce incidente (e quindi verso il cielo) il $\sim$9% della luce totale diffusa, come accadrebbe se fosse applicabile la funzione di diffusione  illustrata più avanti in tabella 2.8. In questo caso lo 0.27% della luce emessa dalla torre viene diffuso nel cielo. Se la pavimentazione a sua volta invia nel cielo il 5% della luce emessa dalla torre-faro, la diffusione contribuisce alla quantità totale di luce inviata nel cielo per circa il 5%. Si tratta di una percentuale non trascurabile, che può crescere molto in caso di maggior densità di aerosoli . Ad esempio in presenza di nebbia moderata il coefficiente di diffusione (v. tabella 2.4) cresce a $2~~10^{-4}~cm^{-1}$ e la quantità di luce diffusa verso l'alto sale al 4.1%. In questo caso la diffusione contribuisce alla quantità totale di luce inviata nel cielo per circa il 45%, quasi la metà. Se l'elevata densità di aerosoli  è presente solo in uno strato a livello del suolo mentre il cielo sopra è limpido, il fenomeno descritto contribuisce notevolmente all'inquinamento luminosoa grandi distanze. Se invece lo strato ad elevata densità di aerosoli  è esteso verticalmente, l'assorbimento e l'estinzione da parte delle particelle fa si che il disturbo provocato  dalla torre-faro decresca rapidamente con la distanza. Perciò, grazie alla maggiore estinzione, un osservatore lontano dalla torre-faro ne sarà meno disturbato del solito mentre un osservatore che si trovi nelle sue vicinanze si troverà ad avere un cielo più luminoso del solito a causa della maggiore diffusione.

La dispersione diretta di luce sopra l'orizzonte e la diffusione di luce tra la sorgente e la superficie illuminata entrano in gioco nel valore del fattore di utilizzazione  K di un impianto. Il fattore di utilizzazione è il rapporto tra il flusso luminoso che cade sull'area da illuminare ed il flusso totale emesso dalla sorgente luminosa. La frazione di flusso luminoso perduta è allora 1-K. Entro questa frazione c'è tutta la luce che va ad illuminare aree che non dovrebbe illuminare. Una parte è legata anche agli assorbimenti nella riflessione sul riflettore dell'armatura e nel passaggio attraverso il vetro di protezione.