
La capacità di vedere le stelle è dovuta non solo alla capacità di rivelare la loro radiazione ma anche al contrasto tra la luminosità della stella e quella dello sfondo.
Knoll et al.
(1946) e Hecht (1947) hanno trovato che un oggetto di dimensione
stellari per
essere visibile contro un fondo di luminosità b ( in nL) deve
produrre una illuminazione i all'occhio (espressa in footcandle) data da:
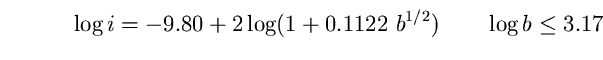
(92)
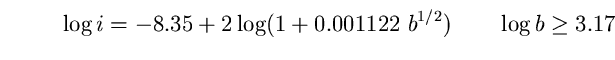
(93)
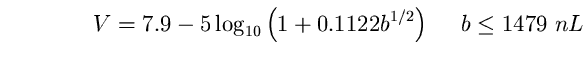
(94)
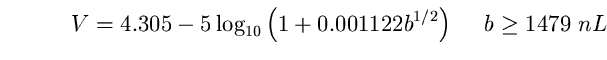
(95)
| brillanza | luminosità | mag. lim. | mag. lim. | 2|c| % stelle visibili | no stelle | |
| nL | vis | appar. | sopra 30 |
|||
| 98.6 | 3.1 107 | 0.0 | 0.0 | 0.02% | 0.03% | |
| 31.8 | 1.0 107 | 1.0 | 1.0 | 0.1% | 0.2% | 3 |
| 8.9 | 2.8 106 | 2.0 | 2.0 | 0.5% | 0.8% | 10 |
| 1.7 | 5.4 105 | 3.0 | 3.0 | 1.7% | 3.0% | 36 |
| 0.057 | 1.8 104 | 4.0 | 4.0 | 6.3% | 11.0% | 130 |
| 3.6 |
1138 | 4.5 | 4.5 | 11.0% | 19.0% | 230 |
| 2.0 |
624 | 5.0 | 5.0 | 19.5% | 33.9% | 400 |
| 1.0 |
324 | 5.5 | 5.5 | 33.1% | 57.5% | 690 |
| 4.9 |
155 | 6.0 | 6.0 | 57.5% | 100% | 1200 |
| 2.1 |
65 | 6.5 | 6.5 | 100% | 2100 |
Note:
Elaborazione su dati di Seares et al.(1925). Il numero di stelle
riportato nell'ultima colonna non è il numero totale di stelle visibili
ma il numero medio di stelle che si possono contare sopra
i ![]() di altezza ed è solo indicativo. Il numero totale di stelle
visibili in un emisfero di cielo fino all'orizzonte è circa doppio.
di altezza ed è solo indicativo. Il numero totale di stelle
visibili in un emisfero di cielo fino all'orizzonte è circa doppio.
A circa ![]() si ha il passaggio dalla
visione extrafoveale (bastoncelli) a quella foveale (coni).
si ha il passaggio dalla
visione extrafoveale (bastoncelli) a quella foveale (coni).
Nell'uso pratico la magnitudine limite va corretta per l'estinzione e la
percentuale di stelle visibili varia di conseguenza.
Esaminiamo ora l'effetto della magnitudine limite sul numero di stelle che si possono vedere a occhio nudo. Il numero di stelle medio per grado quadrato avente magnitudine apparente maggiore di un certo valore m nella banda visuale è stato calcolato da Van Rhijn (1929), Seares et al. (1925) e Seares e Joyner (1928). Moltiplicando per il numero di gradi quadrati dell'emisfero di cielo visibile si trova il numero totale di stelle visibili. Facendo invece il rapporto con il massimo numero di stelle che potrebbe essere visibile a occhio nudo (corrisponde ad una magnitudine limite tra 6.0 e 6.5 a seconda del luogo e della sua estinzione), si può calcolare quale percentuale delle stelle visibili a occhio nudo si può effettivamente osservare con una certa luminosità media o brillanza media del cielo. In presenza di inquinamento luminososcende facilmente a percentuali sotto il 10% come si vede dalla tabella 4.2.
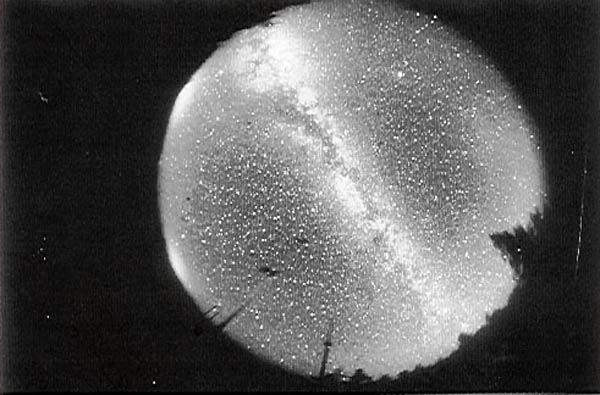
Figure 4.2: La Via Lattea fotografata da un sito non inquinato con un obiettivo grandangolare fish-eye. (Cortesia International Dark-Sky Organization)
L'aspetto della Via lattea, un imponente spettacolo a cui ormai non siamo più abituati, dipende molto dalla luminosità del cielo. La tabella 4.3 descrive la sua visibilità per alcuni valori della luminosità media e della brillanza media del cielo.
| lum. | brill.med. | visibilità a occhio nudo della Via lattea |
| nL | ||
| 1150 | 3.7 10-3 | invisibile; poche centinaia di stelle visibili |
| 500 | 1.6 10-3 | visibile in parte e solo vicino allo zenith, |
| il resto immerso in un cielo grigio luminoso | ||
| 150 | 5 10-4 | contrasto ridotto, perdita dei dettagli fini |
| 80 | 2.5 10-4 | brillante se alta nel cielo ma |
| invisibile avvicinandosi all'orizzonte | ||
| 64 | 2 10-4 | ottima fino all'orizzonte se non c'è foschia |