


Next: Unità fotometriche
Up: Le unità di misura
Previous: Conteggi di fotoni
Spesso è utile considerare la quantità di energia raggiante
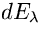 in un certo intervallo di lunghezza d'onda
(
in un certo intervallo di lunghezza d'onda
(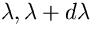 ) che è trasportata attraverso un
elemento di area dA, in una direzione compresa entro l'angolo
solido
) che è trasportata attraverso un
elemento di area dA, in una direzione compresa entro l'angolo
solido 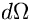 il cui asse fa un angolo
il cui asse fa un angolo 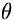 con la normale
alla superficie, in un tempo dt. Si definisce
l'intensità specifica
con la normale
alla superficie, in un tempo dt. Si definisce
l'intensità specifica 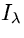 come:
come:
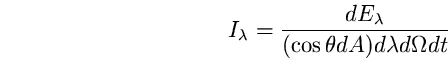
(42)
Si può passare da unità fotoniche ad unità energetiche nel
modo seguente.
Supponiamo che la superficie sia perpendicolare alla direzione da
cui proviene la luce.
L'energia raggiante 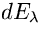 di un flusso di fotoni di
lunghezza d'onda compresa tra
di un flusso di fotoni di
lunghezza d'onda compresa tra 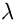 e
e 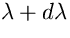 si
può calcolare moltiplicando il numero di fotoni che passa
nell'area dA, nel tempo dt, provenienti dall'area angolare
si
può calcolare moltiplicando il numero di fotoni che passa
nell'area dA, nel tempo dt, provenienti dall'area angolare
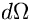 e con lunghezza d'onda nell'intervallo
e con lunghezza d'onda nell'intervallo 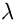 e
e
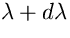 per l'energia di un fotone di quella lunghezza
d'onda:
per l'energia di un fotone di quella lunghezza
d'onda:
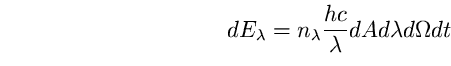
(43)
Quindi
l'energia raggiante totale di un flusso di fotoni di diverse
lunghezze d'onda che viene rivelata da un rivelatore avente una
sensibilità 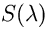 dipendente dalla lunghezza d'onda è:
dipendente dalla lunghezza d'onda è:
![\begin{equation}
dE = \left[ \int S(\lambda)
n_{\lambda}(\lambda)\frac{hc}{\lambda}d\lambda\right] dA d\Omega
dt \end{equation}](images/img168.gif)
(44)
L'espressione tra parentesi rappresenta l'energia raggiante totale
rivelata da un'area unitaria di recettore di sensibilità
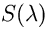 in una unità di tempo da una unità di angolo solido
e si misura in watt per metro quadrato per steradiante
(
in una unità di tempo da una unità di angolo solido
e si misura in watt per metro quadrato per steradiante
(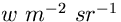 ) oppure in erg per secondo per centimetro
quadrato per steradiante (
) oppure in erg per secondo per centimetro
quadrato per steradiante (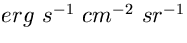 ).
Possiamo
stabilire una costante di passaggio tra unità fotoniche ed
unità energetiche nel modo seguente.
Detta
).
Possiamo
stabilire una costante di passaggio tra unità fotoniche ed
unità energetiche nel modo seguente.
Detta 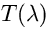 la curva di emissione della sorgente, definiamo
la lunghezza d'onda efficace
la curva di emissione della sorgente, definiamo
la lunghezza d'onda efficace 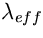 :
:
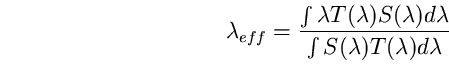
(45)
Possiamo assumere, in prima approssimazione, che
tutti i fotoni emessi dalla sorgente abbiano lunghezza d'onda
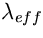 , perciò se S è normalizzata ad 1
l'espressione 3.4
diventa:
, perciò se S è normalizzata ad 1
l'espressione 3.4
diventa:
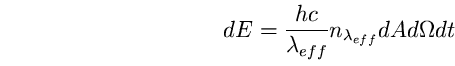
(46)
Assumendo una lunghezza d'onda efficace di 5550
Åper i fotoni della banda astronomica visuale si ottiene con un semplice calcolo
la seguente relazione tra unità energetiche e unità fotoniche:
![\begin{equation}
\frac{dE}{dA_{\perp} d\Omega dt}
\left[ w~m^{-2}~sr^{-1} \rig...
...3.578~10^{-15}
n_{5550} \left[ ph~cm^{-2}~s^{-1}~sr^{-1} \right] \end{equation}](images/img175.gif)
(47)



Next: Unità fotometriche
Up: Le unità di misura
Previous: Conteggi di fotoni
Pierantonio Cinzano
3/12/1998
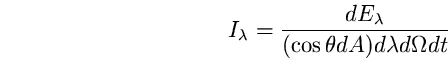
![]() in un certo intervallo di lunghezza d'onda
(
in un certo intervallo di lunghezza d'onda
(![]() ) che è trasportata attraverso un
elemento di area dA, in una direzione compresa entro l'angolo
solido
) che è trasportata attraverso un
elemento di area dA, in una direzione compresa entro l'angolo
solido ![]() il cui asse fa un angolo
il cui asse fa un angolo ![]() con la normale
alla superficie, in un tempo dt. Si definisce
l'intensità specifica
con la normale
alla superficie, in un tempo dt. Si definisce
l'intensità specifica ![]() come:
come:
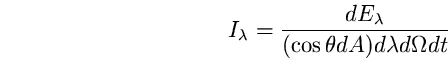
![]() di un flusso di fotoni di
lunghezza d'onda compresa tra
di un flusso di fotoni di
lunghezza d'onda compresa tra ![]() e
e ![]() si
può calcolare moltiplicando il numero di fotoni che passa
nell'area dA, nel tempo dt, provenienti dall'area angolare
si
può calcolare moltiplicando il numero di fotoni che passa
nell'area dA, nel tempo dt, provenienti dall'area angolare
![]() e con lunghezza d'onda nell'intervallo
e con lunghezza d'onda nell'intervallo ![]() e
e
![]() per l'energia di un fotone di quella lunghezza
d'onda:
per l'energia di un fotone di quella lunghezza
d'onda:
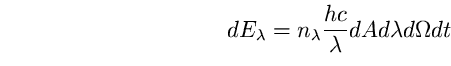
![\begin{equation}
dE = \left[ \int S(\lambda)
n_{\lambda}(\lambda)\frac{hc}{\lambda}d\lambda\right] dA d\Omega
dt \end{equation}](images/img168.gif)
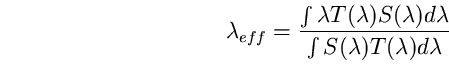
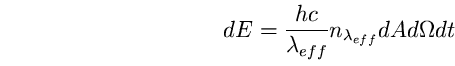
![\begin{equation}
\frac{dE}{dA_{\perp} d\Omega dt}
\left[ w~m^{-2}~sr^{-1} \rig...
...3.578~10^{-15}
n_{5550} \left[ ph~cm^{-2}~s^{-1}~sr^{-1} \right] \end{equation}](images/img175.gif)