Calcoliamo ora
un espressione approssimata per il flusso luminoso ![]() ricevuto
da un osservatore in O in un area di superficie unitaria e
proveniente da un area angolare di cielo
ricevuto
da un osservatore in O in un area di superficie unitaria e
proveniente da un area angolare di cielo ![]() .
.
Consideriamo un volumetto infinitesimo di atmosfera situato lungo la linea di
vista nel punto P alla distanza u da O, ad un altitudine h e di volume
![]() , come illustrato nella figura 2.39.
, come illustrato nella figura 2.39.
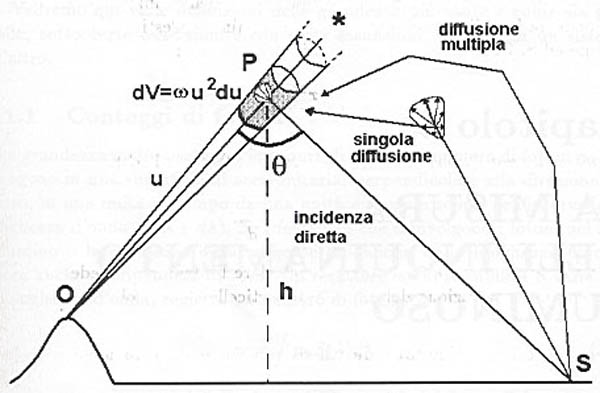
Figure 2.39: Genesi della luminosità del cielo notturno.
Il
volume totale da cui proviene la luce che ha subito diffusione è
l'integrale dei volumi infinitesimi dV .
Nel volumetto considerato arriva, come abbiamo visto, un flusso
diretto per unità di superficie ![]() ove Is è il
flusso emesso dalla sorgente per unità di angolo solido ed
Esp è l'estinzione nel percorso da S a P di lunghezza s. Un ulteriore
flusso per unità di superficie ims arriva dopo aver subito diffusione più volte da
parte delle particelle dell'atmosfera. Quella parte di
quest'ultimo che giunge in P dopo una sola diffusione da parte
degli aerosoli si può stimare, ad esempio, con l'espressione
(2.37).
Come abbiamo visto,
le molecole contenute nel volume dV diffondono la luce incidente
per diffusione Rayleigh (scattering Rayleigh) mentre
gli aerosoli per diffusione di Mie.
Chiamiamo
ove Is è il
flusso emesso dalla sorgente per unità di angolo solido ed
Esp è l'estinzione nel percorso da S a P di lunghezza s. Un ulteriore
flusso per unità di superficie ims arriva dopo aver subito diffusione più volte da
parte delle particelle dell'atmosfera. Quella parte di
quest'ultimo che giunge in P dopo una sola diffusione da parte
degli aerosoli si può stimare, ad esempio, con l'espressione
(2.37).
Come abbiamo visto,
le molecole contenute nel volume dV diffondono la luce incidente
per diffusione Rayleigh (scattering Rayleigh) mentre
gli aerosoli per diffusione di Mie.
Chiamiamo ![]() l'angolo SPO . La sezione d'urto angolare della diffusione Rayleigh sia:
l'angolo SPO . La sezione d'urto angolare della diffusione Rayleigh sia:
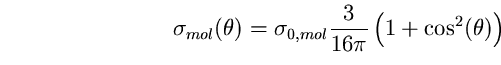
(38)
![\begin{equation}
\Phi=\int \left(E_{SP}\frac{I_{S}}{s^{2}}+i_{ms}\right)
\frac...
...}(\theta)+N_{aer}(h)\sigma_{aer}(\theta
)\right]
\omega u^{2}du \end{equation}](images/img153.gif)
(39)
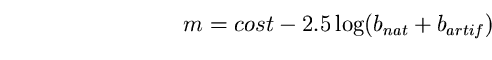
(40)