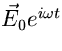 ,
che la polarizza inducendo un momento di dipolo
,
che la polarizza inducendo un momento di dipolo 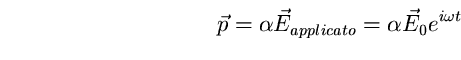
Consideriamo dapprima particelle che siano piccole di dimensioni
rispetto alla lunghezza d'onda della luce visibile. In genere si
comportano come segue le molecole o le particelle di aerosol più
piccole.
In questo caso la particella si può considerare immersa in un
campo elettrico omogeneo periodico 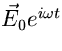 ,
che la polarizza inducendo un momento di dipolo
,
che la polarizza inducendo un momento di dipolo ![]() anch'esso
periodico:
anch'esso
periodico:
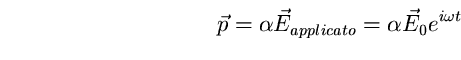
(17)
Per un mezzo in cui la polarizzabilità è uguale in
tutte le
direzioni (isotropo), l'espressione che ci dà l'intensità
della radiazione
dovuta alla diffusione Rayleigh in una data direzione in funzione
dell'intensità del fascio incidente, dell'angolo ![]() tra il
fascio
incidente e la direzione considerata, della polarizzabilità
scalare
tra il
fascio
incidente e la direzione considerata, della polarizzabilità
scalare
![]() , della lunghezza d'onda
, della lunghezza d'onda ![]() e della distanza r è:
e della distanza r è:
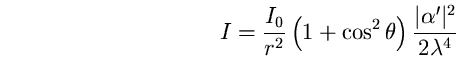
(18)