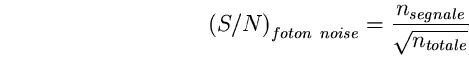
Si definisce rumore qualunque sorgente di incertezza in un
segnale. Ogni stadio del processo di misura della quantità di
luce raccolta da un rivelatore introduce un qualche rumore. Un
problema fondamentale, anche perché dipendente dalle
caratteristiche intrinseche dei fotoni, è il rumore fotonico.
Sotto questo nome si intendono le fluttuazioni casuali nel numero
di fotoni che arrivano al recettore in intervalli consecutivi di
tempo. Si può quantificare il rumore fotonico con la radice
quadrata dello scarto quadratico medio del numero di conteggi. I
conteggi successivi seguono la statistica di Poisson. Se chiamiamo
m il valore a cui tende la media dei conteggi al crescere del
numero di intervalli di tempo considerati, la radice dello scarto
quadratico medio del numero di conteggi tende alla radice di m,
quindi il rapporto tra il numero di conteggi del segnale e il
numero di conteggi del rumore, chiamato rapporto segnale-
disturbo , è:
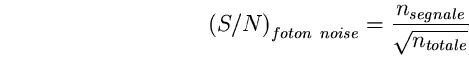
(97)
Torniamo ora al nostro esempio precedente.
Supponiamo che il rivelatore applicato al telescopio abbia un'efficienza del
10% e che il seeing distribuisca la luce della stella, per semplificare,
su un'area circolare di 1 secondo d'arco di raggio ossia su un'area di 3
arcsec2 . In venti secondi il nostro rivelatore riceve, da un'area di cielo
di 3 arcsec2 , 340 fotoni della stella in banda V e 780 fotoni del cielo e
ne "vede", ossia ne conta, 34 della stella e 78 del cielo. Poiché il
segnale è legato al numero di fotoni della stella rivelati e il rumore
fotonico è proporzionale alla radice del numero totale di fotoni incidenti,
il rapporto tra segnale della stella ed il rumore per un osservazione di
venti secondi col telescopio e col rivelatore del nostro esempio è:
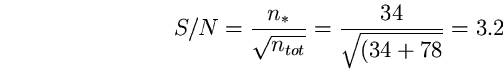
(98)
A parità di tempo di integrazione, lo stesso rapporto segnale-disturbo che si
ottiene con un telescopio di area A ed una brillanza del cielo X volte quella
naturale (nsky ), si può ottenere con un cielo non
inquinato e un telescopio di
area A/X. Infatti se ![]() :
:
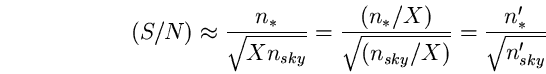
(99)
Il rapporto
segnale-rumore migliora (cresce) al crescere del tempo di integrazione perché sia il numero di fotoni della
stella che quello del cielo crescono allo stesso modo ma il
rumore è proporzionale alla radice del numero totale di fotoni,
quindi cresce più lentamente. Continuando a raccogliere fotoni per t secondi, il rapporto segnale-disturbo dell'osservazione del nostro esempio aumenterebbe di un fattore ![]() .
Tuttavia il numero totale di fotoni raccolti
non può superare il livello di saturazione del rivelatore. Perciò si
può continuare a raccogliere fotoni solo per un tempo limitato
che dipende dal numero totale di fotoni che arriva sul rivelatore.
Se il numero di fotoni che arriva dal cielo è grande, il
rivelatore si satura in fretta.
Chiamiamo
.
Tuttavia il numero totale di fotoni raccolti
non può superare il livello di saturazione del rivelatore. Perciò si
può continuare a raccogliere fotoni solo per un tempo limitato
che dipende dal numero totale di fotoni che arriva sul rivelatore.
Se il numero di fotoni che arriva dal cielo è grande, il
rivelatore si satura in fretta.
Chiamiamo ![]() e nsky il numero di fotoni per
secondo contati dal rivelatore per la stella e per il cielo non inquinato,
nsat il
numero di fotoni massimo prima della saturazione del rivelatore, tmax il
tempo di integrazione massimo prima della saturazione del rivelatore e X il
rapporto tra la
brillanza del cielo effettiva e il suo valore naturale. Per la definizione di
tmax è
e nsky il numero di fotoni per
secondo contati dal rivelatore per la stella e per il cielo non inquinato,
nsat il
numero di fotoni massimo prima della saturazione del rivelatore, tmax il
tempo di integrazione massimo prima della saturazione del rivelatore e X il
rapporto tra la
brillanza del cielo effettiva e il suo valore naturale. Per la definizione di
tmax è ![]() , da cui:
, da cui:
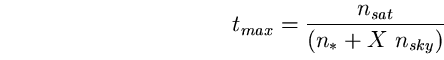
(100)
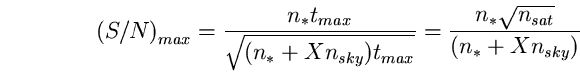
(101)
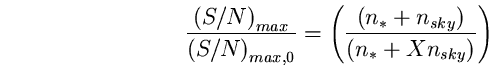
(102)
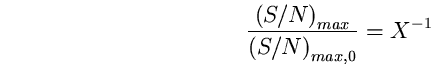
(103)
Gli strumenti nello spazio pur godendo di un migliore potere risolutivo limitato soltanto dalla qualità delle ottiche e dalla diffrazione prodotta dalla apertura finita dello strumento per la mancanza dei limiti imposti dall'atmosfera e pur essendo immuni (per ora) dall'inquinamento luminoso, soffrono dell'impossibilità di inviare nello spazio strumenti con ampie aperture paragonabili a quelle dei telescopi a terra che restano quindi sempre più ``potenti'' ove si tratti di osservare oggetti deboli. Inoltre non è possibile inviare nello spazio un numero di telescopi sufficiente a coprire le necessità di osservazione della comunità astronomica attualmente svolte dai telescopi a terra.