
Le formule illustrate nel paragrafo 4.1.1 esprimono il fatto che la curva della brillanza del cielo prodotta dalla luce dispersa da una città decresce con la distanza da questa con una pendenza piuttosto elevata. Ad esempio la legge di Walker esprime il fatto, come abbiamo visto, che il parametro Q decresce, con il reciproco della distanza elevata alla 2.5. Questa elevata pendenza può ingenerare talvolta l'errata impressione che, in territori ove non vi siano grosse metropoli capaci di produrre inquinamento luminosograndi distanze, solo le sorgenti di inquinamento luminoso situate nelle vicinanze di un sito siano responsabili della luminosità artificiale del cielo in quel sito. In questo ragionamento si trascura il carattere addittivo dell'inquinamento luminoso, ossia il fatto che la luminosità del cielo prodotta da più sorgenti, nel nostro caso più città, si somma. Questo fenomeno è meno appariscente in aree del globo ove la popolazione è radunata in grandi città, ma è fondamentale in aree, come ad esempio la pianura padana, ove la popolazione è distribuita in un miriade di città, paesi e paesini in modo tale da coprire pressoché interamente il territorio. In questo caso, come vedremo nell'esempio più sotto, la frazione della brillanza del cielo prodotta da tutta la popolazione residente oltre una certa distanza dal sito decresce al crescere di questa distanza in modo molto lento. Ciò significa che zone di territorio anche molto lontane dal sito possono contribuire notevolmente alla luminosità del suo cielo. Ciò implica quindi che norme per la protezione di un sito devono poter agire anche su impianti di illuminazione situati a distanze notevoli da esso, pena l'inefficacia delle norme stesse.
Per comprendere le precedenti affermazioni calcoliamo la luminosità del cielo allo zenith di un sito prodotta da tutta la popolazione residente oltre una certa distanza d dal sito stesso. Assumiamo per semplificare che nel territorio considerato la popolazione sia distribuita in modo omogeneo con una densità di p anime per unità di superficie. Questo non è esattamente la situazione della pianura padana ove la popolazione è distribuita in paesi e paesini ma essendo questi sparsi in modo diffuso nel territorio, il nostro modello si avvicina in qualche modo alla situazione reale. Assumiamo inoltre che sia valida nell'area una legge I=p f(r) che fornisce la brillanza I allo zenith in funzione della distanza r da una città avente una certa popolazione p e che questa legge si possa applicare ad ogni area unitaria di territorio di popolazione p.
L'area di un settore circolare infinitesimo di spessore dr posto
alla distanza r dal sito sarà ![]() e la sua popolazione
totale sarà
e la sua popolazione
totale sarà ![]() . La brillanza del cielo prodotta nel sito da
quel settore infinitesimo sarà dunque:
. La brillanza del cielo prodotta nel sito da
quel settore infinitesimo sarà dunque:

(85)
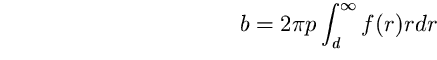
(86)
Facciamo un esempio. Supponiamo di voler proteggere dall'inquinamento luminosoosservatorio
creando una zona di rispetto di 20 km di raggio ove l'illuminazione sia regolamentata. Supponiamo inoltre che attorno all'osservatorio per un raggio di 5 km non ci siano sorgenti importanti di inquinamento luminosoè il caso di un osservatorio isolato, ad es. in campagna o in collina). Il contributo alla brillanza allo zenith proveniente dalla zona oltre i 20 km rispetto al totale, cioè al contributo proveniente da oltre 5 km è:
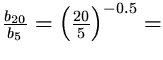 50 %
In conclusione la norma potrebbe influire solo sulla metà della brillanza artificiale del cielo allo zenith dell'osservatorio.
50 %
In conclusione la norma potrebbe influire solo sulla metà della brillanza artificiale del cielo allo zenith dell'osservatorio.