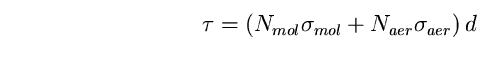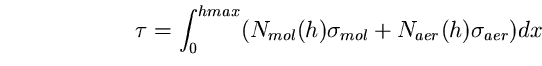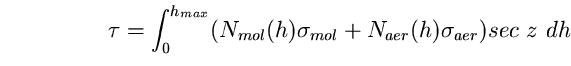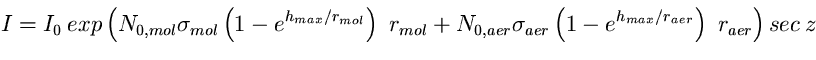


Next: Luce che ha subito
Up: La luminosità artificiale
Previous: La luminosità artificiale
La luce che incide sulle molecole e sulle particelle di aerosoli che si
trovano nel punto P lungo la linea di vista di un osservatore del cielo, e che
proviene direttamente dalla sorgente, ha subito lungo il percorso una
variazione di intensità chiamata estinzione dovuta al fatto che parte
della luce è stata diffusa in altre dirazioni dalle particelle atmosferiche
incontrate nel suo cammino.
La variazione di intensità della radiazione che attraversa per una lunghezza dx un
mezzo contenente N particelle per unità di volume aventi sezione
d'urto integrata 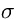 è:
è:

(27)
Integrando si ottiene:

(28)
Nel caso di una radiazione che attraversa uno strato di atmosfera occorre
distinguere il contributo delle molecole e degli aerosoli e
la precedente diventa:

(29)
con
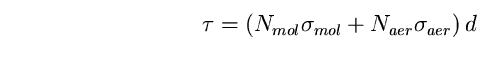
(30)
ove 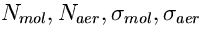 sono rispettivamente la densità numerica di molecole e aerosoli e le loro sezioni d'urto integrate.
In un modello di atmosfera realistico la densità numerica di
molecole Nmol e di aerosoli Naer non è costante ma varia con l'altezza h
per cui:
sono rispettivamente la densità numerica di molecole e aerosoli e le loro sezioni d'urto integrate.
In un modello di atmosfera realistico la densità numerica di
molecole Nmol e di aerosoli Naer non è costante ma varia con l'altezza h
per cui:
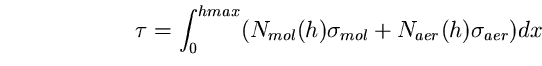
(31)
Poiché 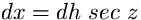 ove z è l'angolo tra la direzione della
luce e la verticale, si può scrivere anche:
ove z è l'angolo tra la direzione della
luce e la verticale, si può scrivere anche:
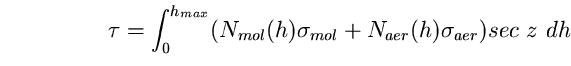
(32)
Se si approssima la distribuzione verticale degli aerosoli e delle
molecole con due funzioni esponenziali aventi raggi di scala
rmol e raer rispettivamente, la espressione precedente
si può integrare e la espressione (2.29) diventa:
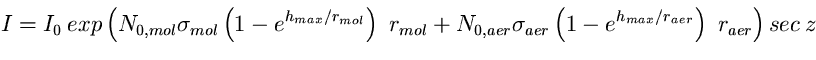
(33)
ove I0 è l'intensità della radiazione emessa dalla sorgente. In
termini di flusso per unità di superficie i (illuminamento) nel punto P prodotto dalla luce proveniente direttamente dalla sorgente S, l'espressione (2.29) si scrive:

(34)



Next: Luce che ha subito
Up: La luminosità artificiale
Previous: La luminosità artificiale
Pierantonio Cinzano
3/12/1998

![]() è:
è: